
- Arithmetic and geometric sequences and series series#
- Arithmetic and geometric sequences and series free#
(We could also try to identify a recursive definition of this sequence. Question 3: Is it necessary for a sequence to. Given two terms in an arithmetic sequence find the common difference, the term named in the.
Arithmetic and geometric sequences and series series#
The sum of the 41st to the 49th term of the AP is 2052.A sequence $\ + (n-1) d = 1 +(n-1) (-4) = - 4n + 5.$$ In contrast, the geometric sequence is the one that deals with the ratio between two consecutive terms constant. Arithmetic & Geometric Sequences & Series Practice. The common difference is added to each term to get the next term. This difference is called a common difference. In an arithmetic sequence, the difference between one term and the next is always the same. What is the sum of the 41st to the 49th term of the arithmetic sequence? Arithmetic and Geometric Sequences sequence is a list of numbers or objects, called terms, in a certain order. The first term of an arithmetic sequence is 8 and the sum of its first 9 terms is 252. 13.5 Sums of Infinite Series Objective To identify an arithmetic or geometric sequence and find a formula for its n-th term 2. The 18th term common to both the sequences is 532. What is the 18th term common to both the sequences? Siyavula's open Mathematics Grade 12 textbook, chapter 1 on Sequences and series covering 1. The first term of another arithmetic sequence is 35 and its common difference is 7. Complex procedures and problem solving are indicated in this Study Guide. (Quadratic sequences form part of the Grade 11 syllabus.) A variety of questions will be asked which will include knowledge and routine procedures, complex procedures and problem solving. The first term of an arithmetic sequence is 24 and its common difference is 4. In mathematics, a geometric progression, also known as a geometric sequence, is a sequence of non-zero numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio. Arithmetic, geometric and quadratic sequences and series are examinable. The 6th term of the geometric sequence is 96. Quiz 1: 5 questions Practice what you’ve learned, and level up on the above skills.

What is the 6th term of a geometric sequence if the difference between its 3rd and 1st term is 9 and that between its 4th and 2nd term is 18? Use this formula to calculate the sum of the first 100 terms of the sequence defined by an 2n 1.

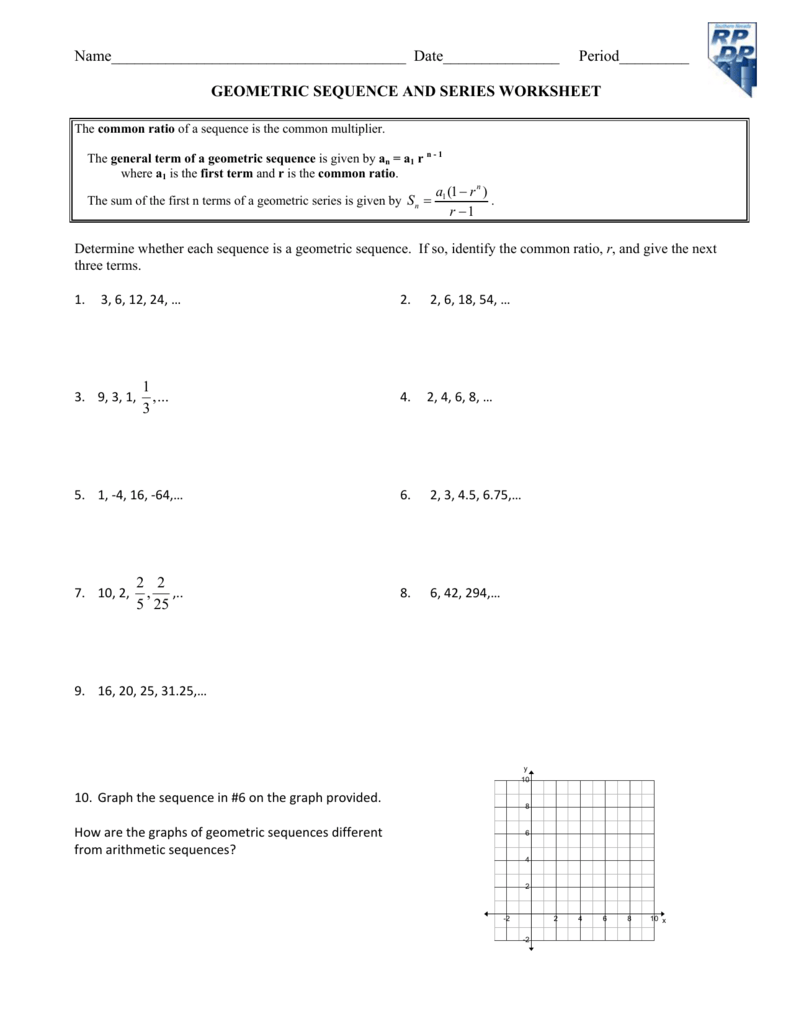
What is the sum of the first 25 terms of an arithmetic sequence if the sum of its 8th and 18th term is 72? 2Sn n(a1 + an) Dividing both sides by 2 leads us the formula for the n th partial sum of an arithmetic sequence17: Sn n(a1 + an) 2. What is 24th term of an arithmetic sequence if its 11th term is 29 and its 31st term is 169? If the term-to-term rule for a sequence is to multiply or divide by the same number each time, it is called a geometric sequence, eg 3, 9, 27, 81, 243. You may also be tested on series and sequence defined by a rule.
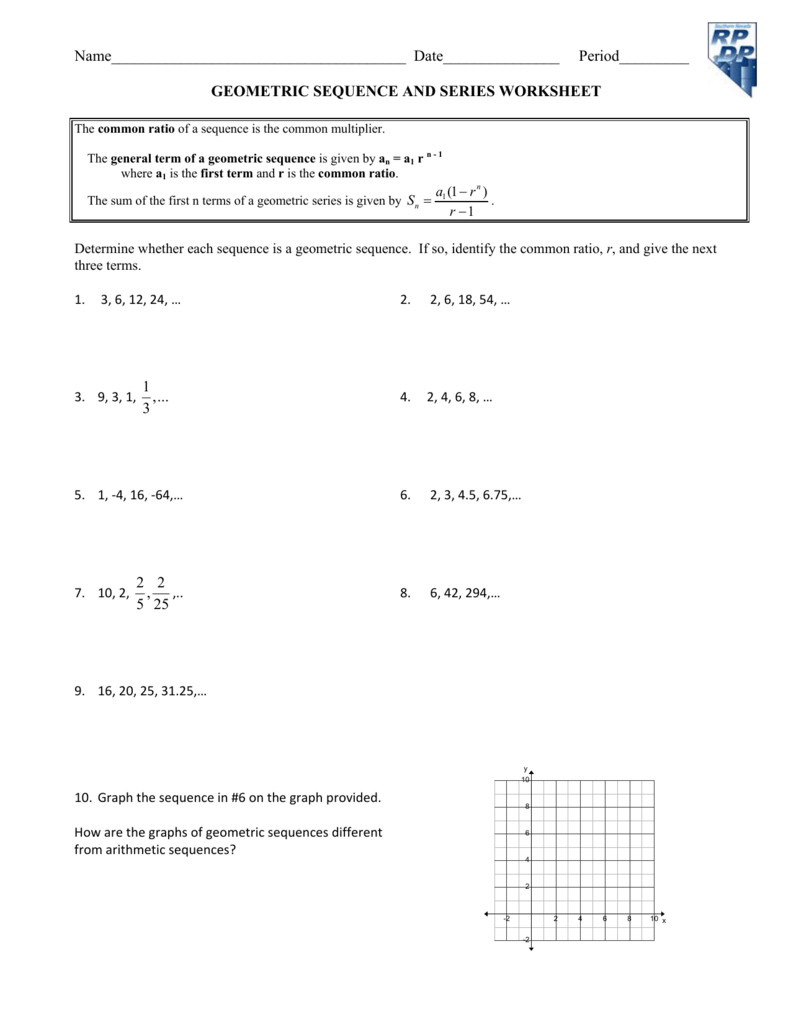
Arithmetic and Geometric sequences are tested and includes the following concepts : sum of sequence, average of sequence, finding a specific term of a sequence, terms common to two sequences, and questions combining terms that may be part of both an arithmetic progression and a geometric progression.
Arithmetic and geometric sequences and series free#
The following is a list of free SAT Practice questions that typically appear from sequences and series. The graph for an arithmetic sequence is actually a series of points that would sit on a line.


 0 kommentar(er)
0 kommentar(er)
